Learn at Home Activities for Math
Before starting, download and print worksheets needed for some of the exercises below.
Here is a link to some general information about number sense.
Here are some short videos explaining important principles to keep in mind when working on counting with your child. Plenty of practice in all different ways will help your child understand these principles.
What are the Five Principles?
One-to-one principle
Stable-order principle
Cardinal principle
Order irrelevance principle
Abstraction principle
Below are some activities to work on the one-to-one principle:
Begin by having your child match one object to one object. Gather small objects such as blocks, Cheerios, rocks and pom poms and ‘vessels’ to put them into such as ice cube trays, muffin trays, cups, ten frame (printable version attached or make your own like the one in the picture using a cookie sheet and masking tape).

Give your child a collection of objects with a few more than the number of ‘vessels’ you are using. For example, if you are using a muffin tray with 12 cups, give them 14-16 objects. If this is difficult, you can start with the exact number of objects. It can also be helpful to use objects that fill the hole; otherwise your child might be tempted to put several in each hole. This activity is meant to work on matching 1 for 1; they do not have to count the objects, just match them up so that each spot gets one object. Other ways to practice this skill:
- Assemble a group of dinosaurs and give them each a piece of Lego dinner.
- Line up a row of blocks and put a toy figure on top of each.
- Gather 8 similar toys and give your child 8 pretend “coins”. Trade a toy for each coin.
- Give your child 6 dolls and 6 hats. They will likely choose to pair them up.
- Put small objects on each square of a checkerboard.
- Ask that every seat at the table get one plate, fork, cup, etc.
When your child is confidently matching 1-1, add counting to above activities. Model counting slowly and touching each object as you count or making it part of the game to say the number at an exact time, like when they release the object. An example of this strategy is shown in this video.
Understand the concept of more and less
Show concrete representations of quantity. Compare groupings of manipulatives and corresponding numbers so that the difference is obvious (ie: stacked like a tower, arranged side by side parallel to each other) and ask which group has more/ less items.
Use a number line and the visual with arrows and the words more and less/ bigger and smaller to show that numbers are bigger/ represent more as you move to the right and smaller/ represent less as you move to the left. Start by using either more/ less or bigger/ smaller and then move to using varied language to describe quantity. Arrange the visual with the dot on a specific number and say:
Tell me a number that is bigger/ more than ___?
Tell me a number that is smaller/ less than ___?
Is ___ bigger/ more than ___? Is ___ smaller/ less than ___?

Point out the arrows and words if they have difficulty deciding. Pair concrete representations such as block towers with the numbers on the number line to illustrate this concept. I have attached a blank template for creating concrete number lines like the one in the picture. Use as is, colour the columns different colours or put fun sticker in each box. Cut the columns apart and have your child put in order from smallest to largest and/ or count the number of boxes or objects and match with the number on the number line to really illustrate the concept of numbers representing bigger quantities as we move from left to right. Ask questions like the ones above: “Which column has more stickers? How many stickers in this column? Can you find a column with more stickers? Less stickers?”
*Make sure your child understands the vocabulary you are using-you may choose to use a different word for column, for example, ‘piece’ or ‘paper’ or ‘strip’.
Understand the process of addition (and subtraction, multiplication, division)
Children need to understand what is happening when performing operations such as addition and subtraction and they need to know why they would choose one operation over another. They need to be able to generalize skills to other contexts as opposed to simply following a script or routine. Therefore, they need lots of practice with concrete representations of these operations. Choose activities that are hands on and realistic. Pair the addition equation with a story that your child will relate to. Draw from their experiences.
Below are a few tips to help them understand the process.
Use the Language Describe what is happening as you work through addition equations. This ladybug activity is a great way to provide a visual representation of an addition equation. Using the language, “How many on this side, how many on the other side, how many altogether’ makes what is happening when we add very clear. The ladybug card can be found here.
Combine Concepts Activities that incorporate more than one concept while remaining ‘step by step’ are great. These bird nests have your child practicing 1-1 correspondence (putting the correct number of eggs in the nest) paired with addition (choosing two nests with eggs already in them and moving the eggs to an egg carton or a basket). These nest cards can be found here.
There are many ways to ‘make’ a number I like the idea of using two different colours to really emphasize the two parts of the addition equation. In this picture, the egg carton is used to explore numbers that add up to ten, so a certain number of one colour ‘eggs’ are placed in the carton (cut to create only 10 holes) and then the carton is filled with a second colour of eggs. A full description of this activity can be found here.
Order doesn’t matter! I have started adding dots corresponding to the numbers on the clothes pegs, allowing for more practice with counting how many and then counting on to find the answer. I also use these sticks to show that 3+2 is the same as 2+3 by leaving the answer peg on and switching the addend pegs around. Talk about how the number of dots didn’t change.
Addition Mat
Use the addition mat provided here (put in a plastic sheet protector to use with dry erase markers) to pair a written equation with concrete manipulatives and then show the action by moving all of the objects to the ‘equals’ column. Use different objects to make up relevant stories. For example, “You have 5 cookies (put five cookies in the first column, while writing the number 5 at the top). I will give you 2 more (put two cookies in the second column while writing the number 2 at the top). How many cookies do you have altogether? (slide all of the cookies over to the last column and have your child count them all).” Before counting, your child may need help lining them up neatly so they are easier to count, or you can provide a bowl to move the cookies into as they count each one.
Understand Ten
Our number system is a base ten system, making the number ten a very important number for children to understand. We can help them to gain access to this important anchor number by teaching what ten looks like and how to construct it in various ways. Knowing the addition facts that make ten also helps the child learn the corresponding subtraction facts.
Rainbow Facts to Ten
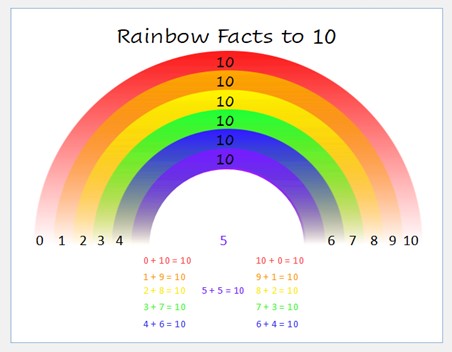
This strategy provides the learner with both a visual to help them recall these facts as well as a label to help them attach the concept in their memory. Spend time reviewing the Rainbow Facts (provided at the top of this post) by having your child draw or follow the colour lines between the number pairs. Provide addition equation frames (also provided) and have your child look at the rainbow visual to find the number pair. Put in a plastic sheet protector and use a dry erase marker to fill in one number.

10 Frame
A 10 frame is a great tool for teaching several important numeracy concepts. Anchoring a complete (full) 10 frame with the number 10 allows the learner to see other numbers in relation to 10. For example, they can see that half of a 10 frame is 5, and two ‘fives’ will fill the 10 frame, or ‘make 10’.
Here is a link to an article about using ten frames (see here also) While this video shows valuable use of the ten frame for understanding addition, it is important to make sure your child understands that the ten frame, when full, will always show ten objects, so spend lots of time changing the orientation of the full board as well as changing the objects you use in the ten frame. Each time, ask “how many?”. When your child consistently answers 10 without counting, move to recognizing another key number, 5. In the same way, explain that one row holds five objects. Fill five boxes, count them, move them and change them many times. When your child consistently answers ‘five’ when asked “how many?”, you can move to other numbers. 4, 6, or 9 are good ones to work on next. To teach 9, for example, show 10, ask how many, then take one object away. See if your child knows that 9 is one less than 10. If they don’t, count the objects together, then show 9 in relation to 10 on a number line. Reinforce using language such as “9 is one less than 10, 9 is almost 10, when the ten frame has one empty spot, we know there are 9 objects, etc.” After practice with 9, move back and forth, showing 10, 5 and 9 objects and asking, “how many?”. Make sure your child is confident naming these visual representations before moving to learning another number.
Make 10 Go Fish
When your child is confidently naming pairs that make ten in other activities, try this game.
It is basically Go Fish except that the object is to find pairs of cards that make ten. For this game, I always post a sentence frame for students to use as they play.
“I have 2. Do you have an 8 to make 10?”
Pyramid Game
First, remove all face cards (except Ace, which will represent the number one) and jokers and shuffle well. Then arrange your cards into a Pyramid with 6 rows, 5 rows face down and the sixth row face up, as shown below, with each row slightly overlapping the previous row.
Place remaining cards in a deck, face down, off to the side.
The goal is to remove cards in the pyramid by “making ten” with two cards. (Or removing a ten card, as it is already equal to ten). Keep the cards you have removed. However, you can only remove cards that are completely uncovered. Once a card is uncovered, turn it over so that you can see it is ‘in play’. Therefore, at the start of the game, you can only use the bottom row of the pyramid to make ten.
No two cards remaining could make ten, but the game is not over! Remember the deck of cards off to the side? These can be drawn from to try and find a needed card. So when there is no other option in your pyramid, draw a card from the deck.
Continue to draw until you can make another ten. Remove those cards and continue to play in the same way. If you make it through the entire deck, you can flip them over and begin drawing again. The game is over when you can no longer remove cards from your pyramid.
To Win the Game: Once you are stuck and can no longer remove any more cards, count the cards you have collected. The person with the most cards wins!
Finally, here is a link to a great article by Rhonda Faragher, who has internationally recognised expertise in the field of mathematics education for learners with Down syndrome, with some tips we can try to apply in many different math contexts.
